Setelah sebelumnya kita membahas Apa itu Regresi, Klasifikasi, dan Clustering, sekarang kita akan membahas salah satu jenis regresi, yaitu simple linear regression dan konsep regresi linear itu sendiri.
Simple linear regression atau regresi linear sederhana merupakan jenis regresi yang paling sederhana karena hanya melibatkan satu variabel bebas atau variabel independen X. Misalnya pada contoh di bawah ini, kita hanya melibatkan variabel engine-size untuk menentukan harga mobil.

Untuk memahaminya, saya telah memplotkan variabel engine-size dan price ke dalam scatter plot menggunakan seluruh data yang ada di dataset automobile. Dataset lengkapnya dapat diakses disini.
Scatter plot menunjukkan dengan jelas hubungan antarvariabel serta sebarannya di dataset. Selain itu, dengan scatter plot di atas juga kita dapat mengindikasikan bahwa variabel engine-size dan price memiliki hubungan linear.

Dengan regresi linear, kita menyelaraskan garis lurus yang melewati data atau istilah di machine learning-nya adalah fit the line untuk mendapatkan model regresi dengan error minimum. Model yang baik dapat digunakan untuk memprediksi perkiraan harga mobil.
Baca juga: Perbedaan Supervised dan Unsupervised Learning
Lalu bagaimana caranya kita menggunakan garis lurus tersebut untuk memprediksi harga mobil?
Misalnya, seperti pada data paling bawah pada gambar tabel di atas, kita akan memprediksi harga mobil dengan engine-size 131. Jika kita lakukan secara manual, kita cukup menarik garis bantu ke atas di titik 131 hingga menempel garis, kemudian tarik garis bantu tersebut ke kiri untuk mendapatkan perkiraan harganya seperti pada gambar di bawah ini.

Dari gambar di atas, untuk engine-size 131 maka perkiraan harga mobilnya berkisar di angka 15000.
Konsep regresi linear
Pada dasarnya konsep regresi linear ini berasal dari persamaan garis. Perhatikan formula regresi llinear sederhana berikut.
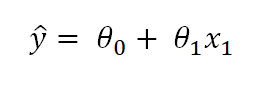
Jika kita melihat formula regresi linear di atas, kita pasti ingat rumus persamaan garis yang pernah dipelajari di bangku sekolah, yaitu y = mx + c, dimana m merupakan gradien atau kemiringan garis dan c merupakan konstanta.
Baca juga: Pengenalan Machine Learning atau Pembelajaran Mesin
Secara umum, model regresi linear dapat diartikan sebagai penggunaan fungsi garis lurus sebagai acuan untuk memprediksi data seperti pada contoh gambar sebelumnya di atas.
Pada persamaan di atas, y_topi merupakan variabel dependen dari nilai yang akan diprediksi, sementara x1 merupakan variabel independen atau variabel bebas atau prediktornya.
Untuk menghasilkan garis yang tepat dengan dengan error seminimal mungkin, kita harus menentukan nilai theta0 dan theta1 yang digunakan sebagai parameter. theta0 merupakan sebuah intersep (intercept), sedangkan theta1 merupakan gradien atau kemiringan garis. theta0 dan theta1 dapat disebut juga koefisien persamaan linear.
Baca juga: 3 Contoh Penerapan Data Formatting dengan Pandas
Pada sumber lain, mungkin kita akan menemukan rumus yang berbeda dalam menotasikan fungsi regresi linear, namun pada dasarnya konsepnya tetap sama. Misalnya mungkin ada referensi yang menotasikannya dengan y = wx + a atau yang lainnya. Dalam rumus y = wx + a, w merupakan gradien dan a merupakan intersep, jadi sama saja kan.
Menentukan nilai parameter θ (theta)
Penentuan nilai theta0 dan theta1 sangat berpengaruh terhadap baik atau buruknya model regresi linear. Untuk mendapatkan nilai theta0 dan theta1 , kita dapat menggunakan pendekatan matematika yaitu dengan menggunakan rumus seperti di bawah ini.


dimana xi merupakan data pada variabel x, yi merupakan data pada variabel y, x_bar merupakan nilai rata-rata variabel x, y_bar merupakan nilai rata-rata variabel y.
Baca juga: 3 Metode Normalisasi Data di Pandas Python
Sebagai contoh, misalnya kita akan membuat model regresi linear dari 6 data di bawah ini. Saya sengaja mengambil sedikit contoh menggunakan sedikit data agar prosesnya dapat dipahami.
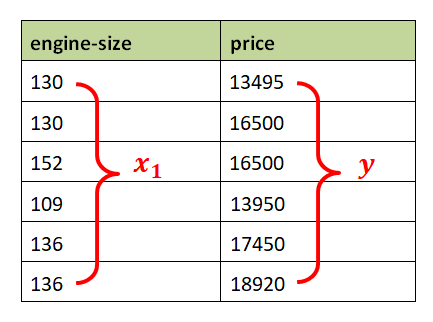
Pertama, kita cari nilai x_bar dan y_bar terlebih dahulu karena diperlukan dalam perhitungan nilai theta0 dan theta1 . Mencari nilai x_bar dan y_bar yang merupakan nilai rata-rata x dan y dilakukan dengan cara menjumlahkan seluruh data pada masing-masing variabel, kemudian membaginya sebanyak data tersebut.
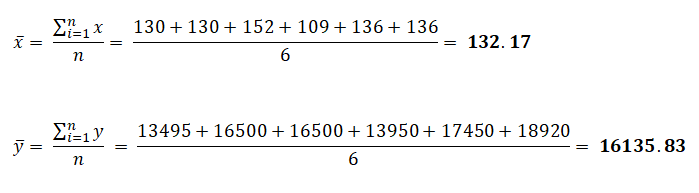
Setelah nilai x_bar dan y_bar diperoleh, selanjutnya hitung nilai theta1 dan theta0 menggunakan rumus di atas.

Setelah memperoleh nilai theta0 dan theta1, kita dapat memasukkannya ke dalam fungsi regresi linear sehingga menghasilkan fungsi berikut:

Lalu, bagaimana caranya kita menggunakan model di atas untuk memprediksi harga mobil berdasarkan engine-size? Caranya cukup mudah, yaitu sesederhana menyelesaikan persamaan tersebut dengan memasukkan data engine-size tertentu.
Misalnya kita ingin memprediksi harga mobil yang memiliki engine-size 133. Kita cukup mengganti nilai x1 dengan 133, kemudian menghitungnya.
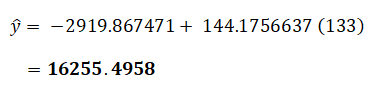
Dari hasil di atas, maka untuk engine-size 133 diperkirakan harganya sekitar 16255.
Regresi linear dengan Python
Dalam prakteknya di Python, kita tidak perlu menghitung seperti cara di atas. Ada library yang dapat digunakan untuk membuat model machine learning yaitu scikit-learn. Library scikit-learn ini mengandung banyak method untuk memudahkan proses pemodelan, salah satunya adalah linear regression.
Pemodelan regresi linear dengan Python
from sklearn.linear_model import LinearRegression
train_x = df_train[['engine-size']]
train_y = df_train[['price']]
regr = LinearRegression()
regr.fit (train_x, train_y)
Kita juga dapat mengetahui nilai dari dua parameter regresi linear theta0 dan theta1.
print('Coefficients: ', regr.coef_)
print('Intercept: ', regr.intercept_) Semoga bermanfaat!
Jika Anda yang sedang belajar data science atau mengolah data dengan bahasa pemrograman Python namun masih suka bingung menulis kode Python-nya, kami telah menyusun Paket E-modul Python Data Science yang didesain khusus untuk pemula dengan penjelasan bahasa Indonesia yang lengkap untuk setiap blok kode-nya. Dapatkan sekarang juga dengan klik di sini!







